社労士の勉強をずっと続けているとさすがに飽きてくるので、気分転換に正月休みに少し毛色の違う本買ってきて読書をしています。
購入した本は世界標準の経営理論(入山章栄 著)です。
かなり厚い本なのでまだ半分ほどしか読み終わっていませんが、この本の中に掲載されている経済学の「ゲーム理論」について、複占(Duopoly)市場における「クールノー均衡」を簡単な数値例で確認したいと思います。
数値例は上記書籍のP157の 注5を使用しています。
なお、「クールノー均衡」では、プレーヤーが自社の生産量を通じて利潤最大化を図るモデルとなります。
目 次
数値例の解説
費用関数と需要関数
まず、企業1と企業2の費用関数と(逆)需要関数を下記の通り想定します。
| 企業1の費用関数 ⇒ C1=10Q1 ・・・① |
| 企業2の費用関数 ⇒ C2=10Q2 ・・・② |
| 需要関数 ⇒ P=100-(Q1+Q2) ・・・③ なお、Q=Q1+Q2 |
上式の①及び②において、Q1、 Q2はそれぞれ企業1、企業2の生産量、係数の「10」は1単位当たりの生産費用(=限界費用)を表しています。また、2社は同じ費用関数を持っています。
③は市場の(逆)需要関数で、縦軸に市場価格(P)、横軸に数量(Q)をとって、経済学のお馴染みのグラフで表現すると、右下がりの直線になります。この需要関数は、市場価格(P)が2つの企業の合計生産数量(Q=Q1+Q2)によって左右されることを意味しています。
企業1、企業2の利潤関数
次に企業の利潤を考えます。
企業の利潤(π)=収入―費用です。
収入=市場価格×数量なので、「企業の利潤(π)=市場価格×数量ー生産費用」と表現できます。
企業1の利益(π1)と企業2の利益(π2)は以下のように表されます。
| 企業1の利潤 ⇒ π1=企業1の収入ー企業1の費用 ⇒ PQ1-C1=PQ1-10Q1 ・・・ ④ |
| 企業2の利潤 ⇒ π2=企業2の収入ー企業2の費用 ⇒ PQ2ーC2=PQ2-10Q1 ・・・ ⑤ |
ここで④、⑤に③(需要関数)を代入してPを消去すると、利潤は生産数量の関数として以下のように表されます。
π1=PQ1-10Q1={100-(Q1+Q2)}Q1-10Q1
= 90Q1-Q12-Q1Q2 ・・・ ⑥
π2=PQ2-10Q2={100-(Q1+Q2)}Q2-10Q2
= 90Q2-Q22-Q1Q2 ・・・ ⑦
利潤最大化条件と反応関数
⑥、⑦をそれぞれQ1、Q2で微分して利潤最大化条件(=反応関数)を求めます。
\[\frac{\partial \Pi{_1}}{\partial Q{_1}}=90-2Q_1-Q_2=0 \Rightarrow Q_1=45-\frac{1}{2}Q_2\]
\[\frac{\partial \Pi{_2}}{\partial Q{_2}}=90-2Q_2-Q_1=0 \Rightarrow Q_2=45-\frac{1}{2}Q_1\]
まとめると、以下の通りとなります。
| 企業1の反応関数: Q1=45-0.5Q2 ・・・⑥´ |
| 企業2の反応関数: Q2=45-0.5Q1 ・・・⑦´ |
⑥´と⑦´を連立させて解くと、Q1=45-0.5(45-0.5Q1) ⇔ 0.75Q1=22.5 ⇔ Q1=22.5÷0.75=30
Q1=30を⑦´に代入して、Q2=45-0.5*30=30
したがって、Q1=Q2=30が「クールノー均衡」における企業1、企業2の生産量となり、その時の価格(P)は、100-(30+30)=40となります。
生産数量:30、価格:40の下、各企業の利益(π1=π2)=(40-10)*30=900となります。
直感的(グラフによる)説明
微分のイメージ
「微分」と言うと毛嫌いされる方もいらっしゃいます。
ただ、経済学ではグラフの接線だったり、最適化問題(最大値や最小値を求めること)を扱うケースが非常に多く、これらはことごとく「微分」に関係していますので、微分のイメージだけでも持っておくと良いと思います。
ということで、以下「文系流」(私自身が文系ですので…)にザックリ説明したいと思います。
厳密な説明ではありませんので、この先は前述の数式が理解できる方には不要な説明となります。
今回の計算では微分して利潤関数の最大値を求めています。
(今回のような)「上に凸の関数」は微分によって最大値が、「下に凸の関数」は最小値が求まります。
最大値を求めるには、グラフに接する水平な線(傾きゼロの線)をひいて、対応する生産量を求めればよいことになります。これが、「微分して0とおく」の意味です。(下記の図1)。
今回の例では、相手企業の生産量(企業1にとってのQ2、企業2にとってのQ1)によって自社生産量が影響を受けるので、「微分して0と置く」だけでは最適生産量は1つに決まりません。
なので、企業1の(利潤極大化の)最適生産量を求めるためには、企業2の様々な生産水準(例えば、Q2=0,1,2,3,4,5…)を設定し、それに応じた企業1の利潤関数を多数用意し、その利潤関数を微分すること(微分して0と置くこと)で求めることが考えられます(下記の図2)。
しかし、企業2の生産量は無数にある(※)ので手間が大変です。
※ 本設例では、Q2=0,1,2,3…,99,100と0以上の整数で考えれば無数ではありませんが、5/3とか9.1といった有理数の世界で考えると無数に存在することになります。
そこで数学の「偏微分:記号の∂で表記」(企業2の生産量Q2を定数の様に扱って、Q1について微分する方法)を使って計算することになります。
(微分して0と置いた)傾き0の接線に対応する企業1の生産量(Q1)とその前提となる企業2(Q2)の生産量をプロットしたグラフが、企業1の反応関数になります(下記の図3)。
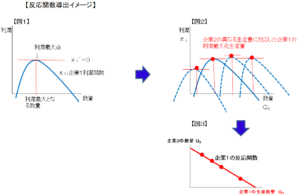
企業2の反応関数についても、企業1の反応関数と同様の手順で求めることができます。
そして、2つの反応関数の連立方程式を解くことで、2つの企業の最適生産量(Q1とQ2)を求めることができます。
クールノー均衡のグラフ表現
2企業の「反応関数」から「クールノー均衡」を求めるプロセスをグラフで表すと、以下のようになります。
-300x127.png)
完全競争との比較
完全競争下においては、企業1と企業2だけでなく、企業3、企業4…と多数企業が市場に参入してきます。
完全競争を想定すると、各企業の費用構造に差はないので、完全競争下における「市場全体の総費用曲線=10*Σ(Q1+Q2+Q3+Q4…)=10Q」となります。
ここで、Qは市場全体の数量を意味します。
また、MC(限界費用)=10なので、供給曲線はP=10となります。
よって、完全競争下の需要曲線と供給曲線の交点の生産量は、P=10=100-Q ⇔ Q=90となります。
結果、完全競争下の均衡価格=10、均衡数量=90となり、完全競争と比べて複占の場合には、数量が少なく(価格が高く)なっていることが確認できます。
グラフで表すと以下の通りです。
-300x237.png)
本日は以上です。



コメント